The Architect of Quantum Mathematics
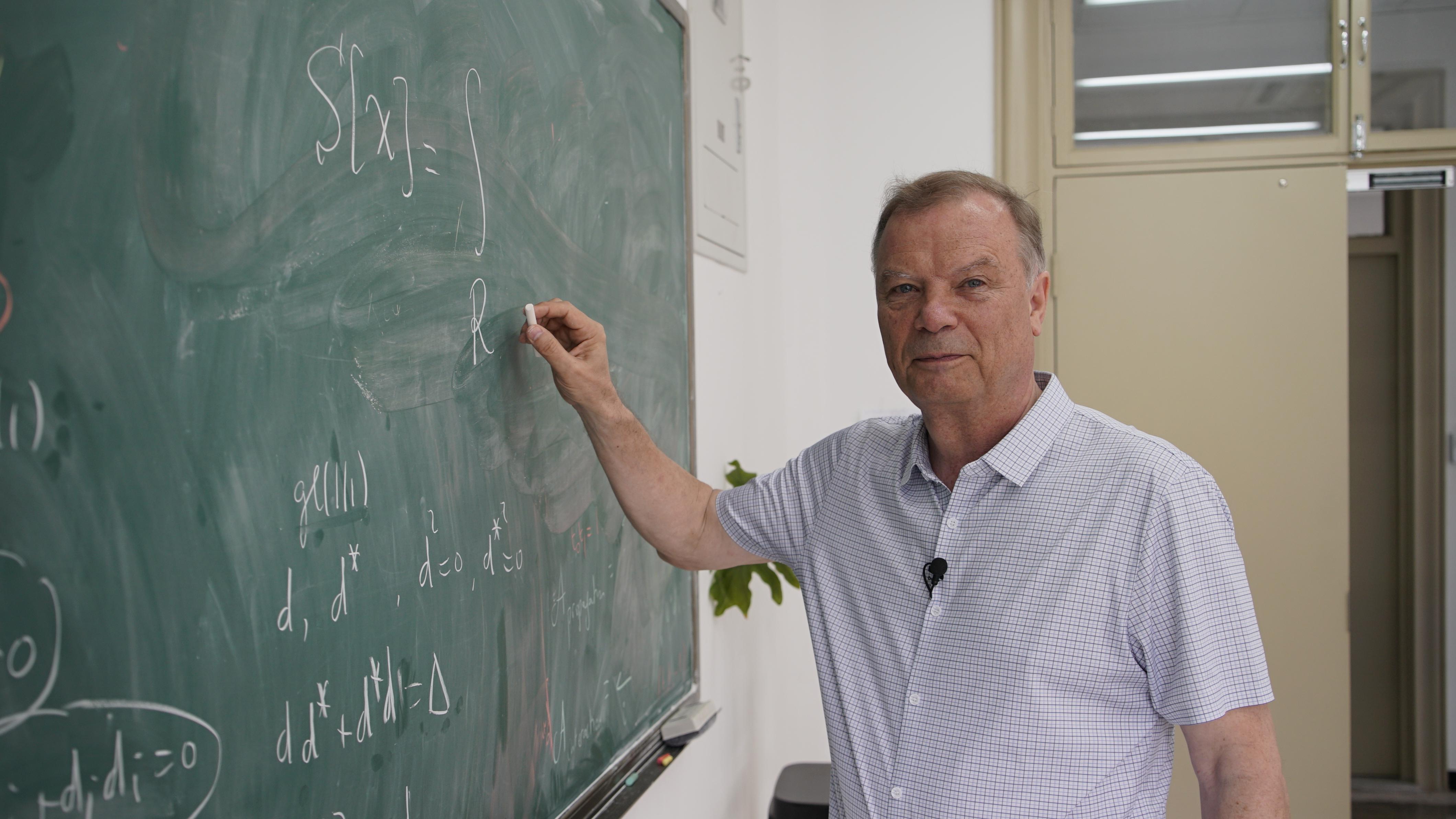
There is a certain old-fashioned elegance in the way Professor Nicolai Reshetikhin teaches. In an age dominated by digital presentations and slide decks, this world-renowned mathematical physicist chooses to write everything on the blackboard, line by line, with meticulous precision.
In 2021, shortly after joining Tsinghua University's Yau Mathematical Sciences Center (YMSC), his handwritten lecture notes went viral on Chinese social media platforms for their clarity, rigor and aesthetic beauty.
Reshetikhin is one of the founding figures of quantum group theory, a pioneer behind the Reshetikhin–Turaev (RT) invariants, a major contributor to quantum integrable systems, and a key figure in advancing our understanding of Poisson geometry and Quantum Kac-Moody algebra. His work bridges abstract mathematical structures with deep physical insights, making him one of the most influential thinkers in modern mathematical physics.
From nuclear engineering to mathematics
When asked how he chose mathematics as his life's work, Reshetikhin explained, "I didn't start as a mathematician. I was in the engineering school, studying nuclear engineering for three years."
This early exposure to applied sciences later shaped his approach to theoretical problems. After shifting to theoretical physics at university, he found his calling in mathematics during an internship at a prestigious mathematical institute. That transition from practical nuclear engineering to the abstract world of quantum symmetries set the stage for a career marked by groundbreaking discoveries.
Quantum groups: hidden symmetries of the universe
One of the most abstract yet fundamental aspects of Reshetikhin's work lies in quantum groups. When asked to explain them simply, he offered an intuitive analogy: "Quantum groups generalize the notion of symmetry. Just as classical symmetry groups describe rotations in space or reflections in crystals, quantum groups describe more complex, hidden symmetries."
These symmetries are not visible in the traditional geometric sense but emerge in quantum mechanical systems. They form the backbone of modern developments in mathematics and theoretical physics. For example, quantum groups underlie the structure of knot invariants, allowing mathematicians to distinguish different knots using algebraic tools. This led directly to the Reshetikhin–Turaev invariants, now a cornerstone of low-dimensional topology.
But their importance extends beyond pure mathematics. Quantum groups appear in conformal field theory, topological quantum computing, and statistical mechanics. Their rich algebraic structure continues to inspire new research across disciplines.
Quantum integrability and the mystery of entanglement
Another major theme in Reshetikhin's work is quantum integrable systems. These rare systems, with a high degree of internal symmetry, often allow exact solutions, illuminating deeper physical principles.
He elaborated: "In many quantum integrable systems, quantum groups describe the hidden symmetries." When asked about the relationship between integrability and quantum entanglement, a topic of growing interest due to quantum computing, Reshetikhin noted that while entanglement is not directly tied to integrability, these systems provide ideal laboratories for studying it.
He highlighted the work of physicists like John Cardy and Vladimir Korepin among many others, who explored entanglement in integrable settings. He also noted China's growing role in this research, where scientists are advancing quantum information and integrability.
The future of mathematical physics
Looking ahead, Reshetikhin identified key open questions in mathematical physics. One is the rigorous formulation of quantum Yang-Mills theory, a Millennium Prize Problem.
"For example, one of the famous Millennium Problems aims to establish a rigorous mathematical foundation for the quantum field theory underlying the Standard Model—specifically, Yang-Mills theory—and more generally, non-Abelian gauge theories."
He called the problem both formidable and fascinating. "Physicists use approximations, but a mathematically consistent theory is still absent."
Most ambitiously, he acknowledged the struggle to reconcile gravity with quantum field theory.
"There are many interesting questions about gravity, like how to fit it with quantum field theory, whether it should remain classical, or whether quantum gravity exists. This debate is not over." He added, "Mathematically speaking, there is close to zero progress in understanding quantum gravity."
Other challenges that he personally wants to address include limit shapes in dimer models on non-bipartite graphs and the link between Poisson sigma models and integrable systems—a conjecture he co-authored, suggesting that wave functions of semiclassical integrable systems can be expressed via Feynman diagrams related to universal two-dimensional Poisson sigma models.
Serving as a bridge
Despite his focus on abstract theories, Reshetikhin sees science as a human endeavor transcending borders. His footsteps have touched many countries to promote global scientific development. "International cooperation is very important. The more exchanges, collaborations, and visits, the better."
Reshetikhin embraces his dual role as a scientist and mentor. "I'm driven by my internal interest in research. I'm very lucky to be actively involved in my career." When asked what he hopes students take from his classes, he replied: "To gain the knowledge and I also teach them to think originally. To be a scientist, you must take the next step from studying to creating something new."
To young researchers who choose between theory and application, he advised: "Follow your curiosity. Fundamental research may seem distant from real-world impact, but history shows the most important breakthroughs come from exploring the unknown."
At the end of the interview, Reshetikhin handed us his handwritten notes to ensure the article's precision and clarity. This small act reflected his traits as a respectable scientist with rigorous dedication and a commitment to advancing public understanding. Reshetikhin bridges disciplines and cultures, proving that science thrives on both brilliance and the willingness to illuminate the path for others.
NIU Yun from YMSC also contributed to this article.